How does the Joola “Propulsion Core” design, with a strip of soft foam around the top/sides, work to increase pop/power?
Since I find it interesting, I thought I’d write a bit about my hypothesis. I have a mechanical engineering degree, but I never took any vibration courses. I probably had some basic introduction, but mostly, I’ve just picked things up from reading papers about coefficient of restitution and the like. I’m far from an expert in this area, and I’d be grateful for feedback from those with more knowledge.
First, a paddle has a first bending mode (FBM) that is similar to that of a free-free beam. The animation below shows the FBM of a simulated, typical paddle. The brightly colored areas indicate the nodes, or places where displacement is minimal, of this vibration mode. You can find these nodes on a paddle by holding the paddle loosely between your thumb and forefinger at approximately the node on the handle. Let the paddle hang vertically and tap up and down the face. The paddle will vibrate more or less, depending on where you strike it. The vibration will be minimal at the node.

The FBM node is a “sweet spot” and, based on my reading about tennis racquets, the most important “sweet spot”. When a ball is struck at the node, no energy is converted into vibration of the FBM, so more energy is returned to the ball. The vibration of the FBM is easy to feel, so a player will naturally attempt to hit the node.
The FBM is too “slow” to return energy to the ball. If a ball is struck between the nodes, you might expect the paddle to act like a trampoline and provide extra energy to the ball as it vibrates back into the ball. It won’t happen, though, as the ball has already left the paddle before it cycles back.
There are vibrations modes that are sufficiently “fast” to return energy to the ball. There is a membrane mode of the paddle face that is approximately centered on the paddle face, as shown in the animation below. The frequency of this membrane mode is probably the most important value for the “trampoline effect” of a paddle. I don’t yet have any data to back this up, but I suspect that on thicker (16+ mm) paddles, the frequency is higher than optimal for energy return, and it becomes more optimal as the thickness, and thus frequency, decrease.
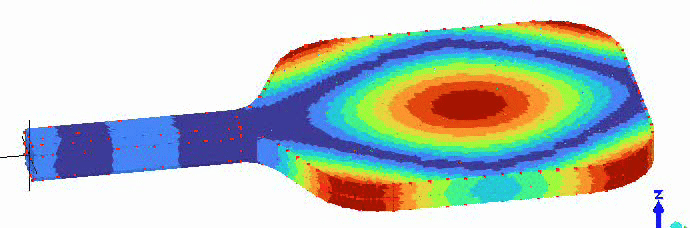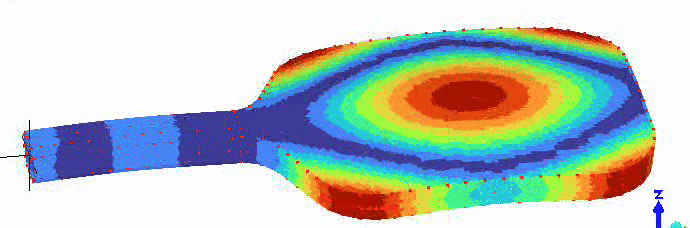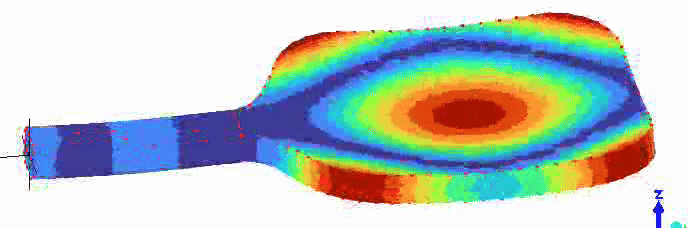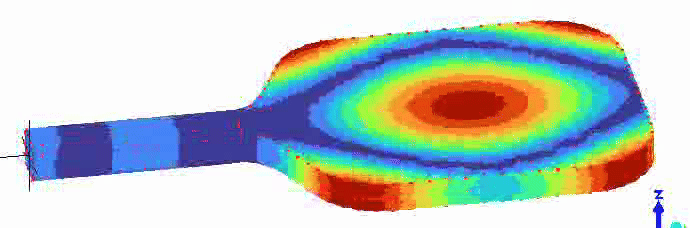
So, how does the foam around the top and sides of the Joola “Propulsion Core” create more power?

In the vibration animations above, notice that the location of the FBM node is higher up the paddle face than the center of the membrane mode. As a result, if you hit the FBM node, you avoid energy loss to FBM vibration, but you don’t get the full benefit of the membrane mode. If you hit the center of the membrane mode, you get the full effect of that mode, but you lose some energy to FBM vibration. What if the two were aligned? I think that’s what the soft foam of the propulsion core achieves. Because the rigid honeycomb portion of the core is shorter, the FBM node will shift down the paddle face and be better aligned with the center of the membrane mode. The new, better-aligned “sweet spot” will also be closer to the paddle center of gravity than a typical “sweet spot” would be, resulting in a higher effective mass for the collision. The result of all that is more energy returned to the ball.
Is that all good news? I’m not sure. When the FBM node and the center of the membrane mode are misaligned, it elongates the area where energy returned is approximately equal. That misalignment may be better for consistency, as if you play anything like I do, you don’t hit the same spot on the paddle every time.
What do you think? I’ve not touched one of these paddles yet. If you have one, does the FBM node seem lower on the paddle face than on a typical paddle? Does it feel like the power falls off more quickly than a typical paddle if you hit near the tip of the paddle? I’d expect it to.

