Since finishing the Android app, I’ve gotten back to a couple of other developments. I mentioned a twistweight adapter in another blog post, and I’ve received some interest in measuring the swingweight of pickleball paddles. In both cases, the measurements are outside the range of typical tennis rackets. I had done some linearity testing when developing the SW1, so I was pretty confident about measuring pickleball paddles. However, the twistweight adapter requires measurements down in the single digits, so I decided to do some testing all the way down to zero.
I fabricated and measured PVC pipe calibration rods at targets of 25, 50, 100, 150, 200, 250, 300, 350, and 400 kg·cm². For all but the three longest pipes, I measured the length with the same calipers (0.002 cm resolution) and fixtures that I use for production, but for the longer pipes, I used a stainless steel meter stick with etched millimeter markings and an eye loupe to estimate to the nearest 0.01 cm. The swingweight of each rod was calculated from the formula for a thick-walled, cylindrical tube with open ends. I used an outside diameter of 3.34 cm, inside diameter of 2.66 cm, and a pivot axis 10 cm from the end. The measurements and resulting swingweight are summarized in Table A.

| Mass (kg) | Length (cm) | Swingweight (kg·cm²) |
| – | – | 0.00 |
| 0.16175 | 34.726 | 25.21 |
| 0.20471 | 40.600 | 50.07 |
| 0.24517 | 48.882 | 100.23 |
| 0.26260 | 55.422 | 149.89 |
| 0.28281 | 60.522 | 202.74 |
| 0.32317 | 62.390 | 250.37 |
| 0.34187 | 65.86 | 303.71 |
| 0.35782 | 68.88 | 355.61 |
| 0.37052 | 71.27 | 400.75 |
With an SW1, I took measurements empty and with each of the calibration rods. PVC pipe is not perfectly homogenous, so I measured each rod in both orientations. For each configuration, I recorded the oscillation period of five measurements and averaged the results. These results are summarized in Table B.
| Swingweight (kg·cm²) | Period A (s) | Period B (s) | Avg. Period (s) |
| 0.00 | 0.17497 | – | 0.17497 |
| 25.21 | 0.39043 | 0.39005 | 0.39024 |
| 50.07 | 0.52219 | 0.52224 | 0.52222 |
| 100.23 | 0.71842 | 0.71842 | 0.71842 |
| 149.89 | 0.87020 | 0.87030 | 0.87025 |
| 202.74 | 1.00840 | 1.00627 | 1.00734 |
| 250.37 | 1.11624 | 1.11681 | 1.11653 |
| 303.71 | 1.22793 | 1.22635 | 1.22714 |
| 355.61 | 1.32378 | 1.32815 | 1.32597 |
| 400.75 | 1.40648 | 1.40619 | 1.40634 |
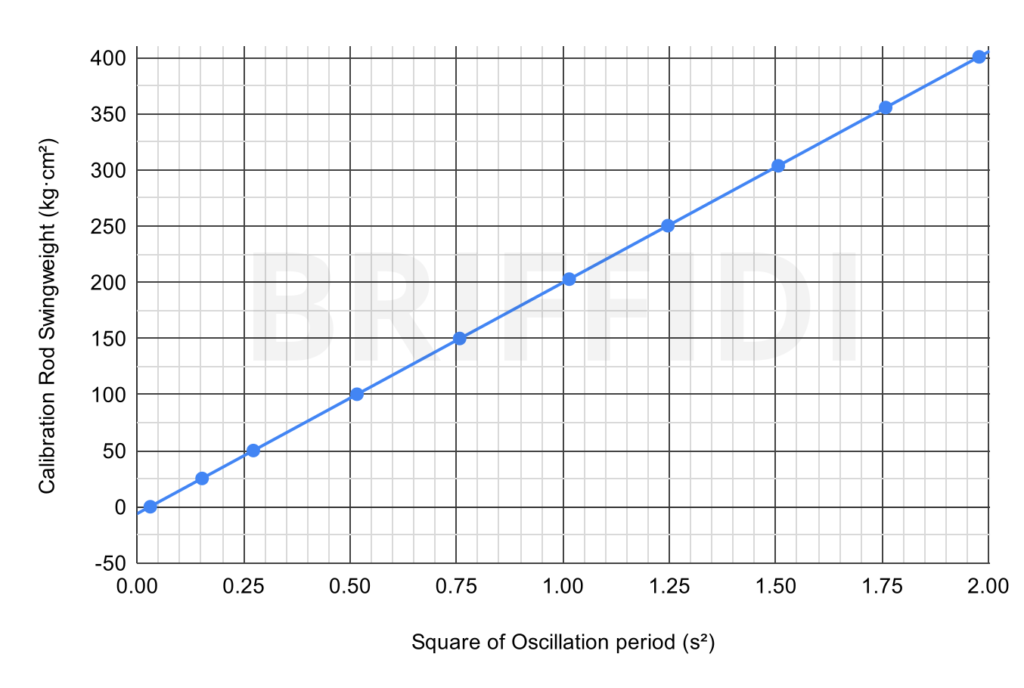
For an oscillating, horizontal spring pendulum as used by the SW1 and most other swingweight machines, the moment of inertia of the system (racket plus oscillating portion of the machine) is proportional to the square of the oscillation period. Figure 2 is a plot of swingweight versus the square of the oscillation period. A linear trend line fits very well. For the curious, the slope and y-intercept of this line are the calibration results displayed at the bottom of the Calibrate page in the app. However, the line is fitted exactly through points at the two calibration values (around 150 and 300 kg·cm²), and the sign of the y-intercept is flipped.
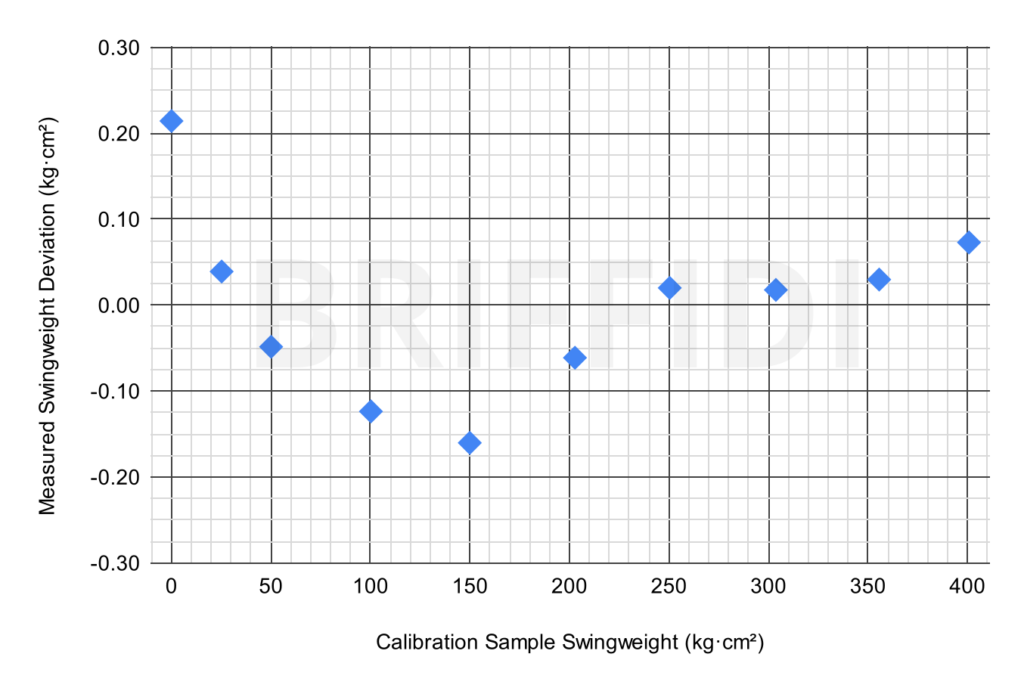
Looking much more closely, Figure 3 shows the deviation of the measured swingweight from the calculated swingweight of each calibration rod. The results of the fitted trend line in Figure 2 are used to calculate the swingweight from the period of oscillation. The first thing to notice is that the largest deviation is only 0.21 kg·cm². Second, the deviation doesn’t look entirely random. I would need to repeat this testing to see if this pattern persists. If it isn’t random, perhaps friction is causing the deviation to increase near zero. I’m not sure what else would cause such a pattern, but please leave a comment below if you have an idea.
When designing the SW1, I calculated the torque deviation introduced by using a linear spring to drive a rotating pendulum. I considered other designs, such as a spiral spring or using a drum and cables to convert linear spring force into torque. In the end, I chose to stick with a simple spring drive but oscillate through a smaller arc than other swingweight machines I’ve seen, as this kept the deviation below 1% at the extremes of travel.
How do these results compare to other swingweight machines? The only similar data I’ve been able to find is from an old Babolat RDC, and it was quite non-linear. I expect that modern machines are better, but I don’t know. I’d be happy to test that. If you’re in the DFW area and have another swingweight machine that I could use for testing, please send me a message at support@briffidi.com.
So, what did I learn?
- The SW1 is very linear from zero to 400 kg·cm² and presumably beyond.
- It’s capable of measuring twistweight very precisely and accurately with the adapter I’m developing.
- It’s suitable for measuring pickleball paddles (with a suitable adapter for mounting the paddle).
- It’s reasonable to calibrate the SW1 with a single calibration object. Did you lose the calibration weight for your SW1? I can replace it, but you could also set the calibration “Object #1” value to zero and take measurements for the first and last groups with only your phone in the cradle. Absolute accuracy may suffer slightly, but using these data and calibrating with the zero and 149.89 kg·cm² measurements, the deviation at 400.75 kg·cm² is still only 0.86 kg·cm².