Tag: twistweight

Posted on by — 2 Comments

Can Twistweight be Too High?

I was watching Episode 42 of the Pickleball Effect podcast while assembling SW1s today, and Braydon asked if it was possible for twistweight to be too high. He went on to mention that he felt that a high twistweight slowed down the acceleration of his backhand flick. I’m a bit surprised that he was able to notice it, but that is an expected effect of higher twistweight.

Consider mass added at the 4 and 8 o’clock positions of a paddle and reference the sketch below. The effect of that mass (m) on swingweight is m·a². For example, if adding 6 g (3 g per side), and a is 18 cm, then the swingweight will increase by (0.006 kg)·(18 cm)² = 1.944 kg·cm². The effect of that mass on twistweight is m·b², so if b is 9.5 cm, the twistweight will increase by (0.006 kg)·(9.5 cm)² = 0.542 kg·cm².

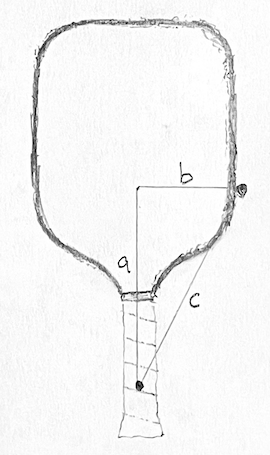
There is a third axis about which moment of inertia is interesting. This has conventionally been called spinweight, and it’s measured about an axis 90 degrees from the swingweight axis. In the sketch above, it would be about an axis coming out of the screen through the vertex a-c. It’s also the axis you’d get by installing a paddle into a swingweight machine with the paddle face parallel to the ground (more on that after the break). The effect of the added mass on spinweight is m·c². Length c is √(a² + b²) = 20.35 cm, so the added spinweight is (0.006 kg)·(20.35 cm)² = 2.485 kg·cm².

Note that the sum of the added swingweight and twistweight is equal to the added spinweight: 1.944 + 0.542 = 2.486 kg·cm². This will always be the case, assuming a paddle is approximately planar, and is described by the perpendicular axis theorem.

Back to Braydon’s backhand flick, there’s a large component of acceleration about the spinweight axis for this shot. Given two paddles, with everything equal except that one has a twistweight of 6.0 kg·cm² and the other has a twistweight of 7.0 kg·cm², the second paddle will have a spinweight that is 1.0 kg·cm² higher. The difference is there, but it’s small.

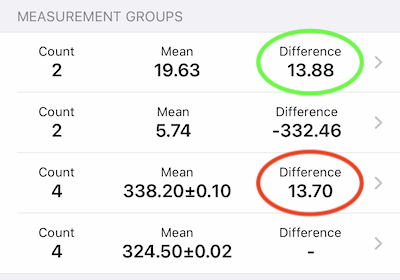
I wanted to add a bit more about measuring swingweight and spinweight in the real world. Theoretically, you could measure both swingweight and spinweight with the SW1. Practically, for paddles, the results are a bit misleading, as the effect of air resistance is very significant in the swingweight orientation. For example, my current main paddle has a swingweight of 114.3 kg·cm² and a twistweight of 7.5 kg·cm², but the spinweight measures 117.7 kg·cm². That’s lower than the expected result of 114.3 + 7.5 = 121.8 kg·cm², but that’s because the swingweight measurement is inflated due to the effect of air resistance. To minimize the effect of air resistance on swingweight, you could measure spinweight and subtract twistweight. In my case, that gives a result of 110.2 kg·cm². Of course, that’s only useful if comparing to paddles measured similarly.

If you’re interested, I have a bit more about the relationship between swingweight, twistweight, and spinweight for tennis racquets in the post Racket Twistweight from Spinweight and Swingweight.

Posted on by — Leave a comment

New SW1 App Features in Open Beta

I recently improved the calibration process in the Briffidi SW1 app. I also added saved tare values to make switching between adapters easier. These features are available to try now in open beta versions of the apps. Install the appropriate app by following one of these links: iPhone Open Beta or Android Open Beta.

Calibration Process

The calibration process for the Briffidi SW1 is confusing to many users. It’s unintuitive and was heavily influenced by the required app development effort. In my defense, I didn’t know if I’d sell many SW1s, and there were many other things to do to release a product. It worked.

Recently, I spent some time figuring out a more intuitive calibration process. Instead of creating measurement groups and taking specific measurements in each group, the calibration measurements are taken directly from the Calibrate tab in the app. There are sections for each configuration of the calibration rod, and each section incudes a dedicated Measure button and a dedicated measurement group.

When there is at least one measurement in each calibration group (I recommend at least two measurements of each), the Calibrate button will become active. After the Calibrate button is tapped, the Calibration Results below will update, and a confirmation will be displayed. If the calibration results are outside of normal ranges, the confirmation will indicate that, the abnormal result will be highlighted in red, and possible solutions will be displayed below. For example, users commonly extend only three of the four internal sections of the extendable calibration rod. When this happens, the Spring Constant result will be abnormally high. The results and confirmation display as shown below.

Things to check are displayed below the results.

Saved Tare Values

As I used the SW1 more with the twistweight and pickleball adapters, I often found myself forgetting to tare out the adapter before mounting a racquet or paddle. To make this process easier, the three latest Tare values are available for recall. When switching back to an adapter you’ve previously tared-out, long-press the Tare button to select the appropriate tare value. Note that the saved tare values are cleared during calibration.

Additionally, it wasn’t always clear that the Tare function was active. Now, when active, in addition to the button being filled in blue, the button text will indicate the value being subtracted from the measurement result.

Feedback Requested

If you try out a beta app and have any problems or suggestions for further improvement, please let me know in an email to support@briffidi.com.

Posted on by — Leave a comment

Replicating My Racquet Handle on a Paddle

I’ve been playing a good bit of pickleball lately, in addition to tennis, and the paddle handles I’ve used aren’t really to my liking. My main tennis racquets are customized Head Gravity Lites with 3D-printed pallets, and I wanted to try replicating that handle on a paddle. I bought a cheap, raw carbon fiber faced paddle (Hisk Rav Pro) to tear apart.

The paddle handle is simply cut from the laminate of face and core materials. Foam pieces are stapled on either side, and there are a couple thin steel sheets under the foam for added weight (9 g for both). A flared butt cap is stapled onto the end. There is foam tape applied all along the edge of the paddle. The resulting handle is pretty squishy, and it lacks the well-defined, octagonal bevels that I’m used to from tennis racquets.

The handle is 31 mm wide, which is just under the corresponding 32.1 mm width of my target. The depth of this surface, at 16.24 mm due to the 16 mm core, is considerably larger though, so the corners exceed the outline of my target. I printed a handle like this.

I used the handle as a guide to file down the corners of the paddle that stuck out.

I added double-sided tape to the handle faces and wrapped the handle tightly with more double-sided tape.

Here’s the result next to one of my racquets. They feel very similar in the hand. And yes, I know my racquet needs a new overgrip.

The printed handle is ~6 grams heavier than everything it replaced, though it could have been lighter. I opted for thicker walls for durability, as I didn’t think I’d mind the extra weight in the handle. Final specs with overgrip and ~13 g of lead just above the bottom shoulders (4 and 8 o’clock):

  • Weight: 252.5 g (8.9 oz)
  • Balance: 22.6 cm
  • Swingweight (5 cm): 115.7 kg·cm²
  • Twistweight: 6.93 kg·cm²
Posted on by — 2 Comments

Racket Twistweight from Spinweight and Swingweight

A commenter recently asked on the Effect of Orientation post whether twistweight is really equal to the difference between spinweight and swingweight. It’s a common approximation based on the perpendicular axis theorem. That theorem is valid for planar (two-dimensional) objects. A tennis racket is nearly planar, but as mass deviates from that plane, twistweight will increase slightly.

To quantify the error, I looked back at the CAD model I had created for the Effect of Orientation post.

Here are the moment of inertia properties from CAD:

  • Swingweight: 306.82 kg·cm²
  • Spinweight: 320.01 kg·cm²
  • Twistweight: 13.58 kg·cm²

The difference between spinweight and swingweight is 320.01 – 306.82 = 13.19 kg·cm². The twistweight is 13.58 kg·cm², so there is an error of -0.39 kg·cm² or -2.9%. As expected, the actual twistweight is higher than approximated. This error will vary based on the accuracy of my CAD model and the geometry of the racket, but it should be somewhat close to that value.

I have a prototype device to measure twistweight more directly (UPDATE: The Twistweight Adapter is available.), as I’ve found a practical issue with determining it from spinweight and swingweight. That issue is a crooked butt cap. When I measure the swingweight of a racket and then flip it 180° and re-measure it, the measured value is often different by tenths of a kg·cm². That’s a small difference in terms of swingweight, but it’s large relative to twistweight determination.

I also have been 3D printing pallets with integrated caps. As seen in the photo, the pallet is two pieces, so the face of the butt end should be nearly perfectly square in the wider direction (affecting swingweight) and perhaps not quite square in the shorter direction (affecting spinweight) if the two halves aren’t perfectly aligned. The door is slightly recessed, so it won’t interfere with measurements.

I measured the racket in the photo using both methods on my SW1. In the first (bottom) measurement group, I measured the swingweight of the racket twice in one orientation and twice at 180°. In the second group, I measured spinweight in the same way. As expected, there was a bit of deviation in the spinweight measurement, likely due to misalignment of the pallet halves. The difference of 13.70 kg·cm² is circled in red. Then, I measured my twistweight device empty and finally with the racket. The more directly measured twistweight of 13.88 kg·cm² is circled in green.

In this sample measurement, there was less difference between the two methods than there was in CAD. I haven’t explored why. There is error in all the measurements, and I haven’t used the prototype twistweight device enough to fully understand its capabilities.

So, back to the original question: is twistweight really the difference between spinweight and swingweight? Not exactly, but it’s a pretty good approximation. Practically, as long as the butt cap of the racquet is square, it’s useful, especially when the goal is to match the twistweight of similar rackets.

Thanks for the question, Ryan.